- Z Transform Example Problems
- Inverse Z Transform Examples
- S To Z Transform
- Z Transform Table
- Z Transform Formula
- Z Transform Equation
- 3 The inverse z-transform Formally, the inverse z-transform can be performed by evaluating a Cauchy integral. However, for discrete LTI systems simpler methods are often sufficient. 3.1 Inspection method If one is familiar with (or has a table of) common z-transformpairs, the inverse can be found by inspection. For example, one can invert the.
- Z-Transform. In general, the ROC R of a z-transform of a sequence gn is an annular region of the z-plane: where. Note: The z-transform is a form of a Laurent series and i l ti f ti t i t i th ROCis an analytic function at every point in the ROC.Example– Determine the z-Transform X(z) of the causal sequence xn= = αn μn and its ROCand its ROC.
- The z-Transform Content Introduction z-Transform Zeros and Poles Region of Convergence Important z-Transform Pairs Inverse z-Transform z. – A free PowerPoint PPT presentation (displayed as a Flash slide show) on PowerShow.com - id: 453666-YmYxZ.
Example 7.3 Left-Sided Signal 10 Determine the z-transform of the signal y n nu n 1. Depict the ROC and the location of poles and zeros of Y(z) in the z-plane.
Have you ever tried your text to fit along the edge of a circle, or even within a circle? Or, on a curved path, or even as a roller coaster? Mostof the time, you need not play as much with words but sometimes if you want to create a quick logo, or even an easy graphic, then you will findPowerPoint's Transform tools for text very useful. Look at Figure 1 below to explore some quick text effects possible right withinPowerPoint.
Figure 1: Examples of Transforms text effect for text
Transform is a special stylizing option available in PowerPoint only for text. Follow these steps to explore more inPowerPoint 2010 for Windows:
- Select the text to which you want to apply Transform texteffect. Alternatively, if you just want to follow this tutorial step-by-step,insert a text box on a blank slide and type some text in it asshown in Figure 2. Select the text, or the entire text box as required to bring up the Drawing Tools Format tab onthe Ribbon as shown highlighted in red withinFigure 2.
Figure 2: Drawing Tools Format tab of the Ribbon- Within the Drawing Tools Format tab, locate the WordArt Styles group. Then click theText Effects button that you can see highlighted in red within Figure 3.
Figure 3: Text Effects button within WordArt Styles group- This opens the Text Effects drop-down gallery, as shown in Figure 4. Select the Transformoption which is the last option in this gallery (shown highlighted in red within Figure 4).
Figure 4: Transform option within Text Effects drop-down gallery- This opens the Transform sub-gallery as shown in Figure 5.
Figure 5: Transform sub-gallery- Let us explore various effects within Transform sub-gallery as marked in Figure 5:
- Removes any transform effect already applied to the selected text.
- These Transform effects make your text to flow in a certain path like a circle, or an arc etc.
- Here you will find Transform effects that twist and turn your text in various directions, and also make them wavy. To explore moreWarp effects, use the scroll bar towards right (highlighted in blue, within Figure 5).
- When you hover your cursor over any of the Transform effects within the Transform sub-gallery, you will see aLive Preview of the effect on your selected text. Click on any effect toapply it to the selected text. In Figure 6 you can see the selected text applied with Chevron Up effect.
Figure 6: Transform Effect applied- Do you notice the pink handle on the left of the text box in Figure 6, above (highlighted in red)? Youcan use that to create more transforms for text. We explain this option in ourAdvanced Text Transforms in PowerPoint 2010 tutorial.Remember to save your presentation often.
A. No Transform
B. Follow Path
C. Warp
- Digital Signal Processing Tutorial
- Operations on Signals

- Basic System Properties
- Z-Transform
- Discrete Fourier Transform
- Fast Fourier Transform
- Digital Signal Processing Resources
Z Transform Example Problems
- Selected Reading
If we want to analyze a system, which is already represented in frequency domain, as discrete time signal then we go for Inverse Z-transformation.
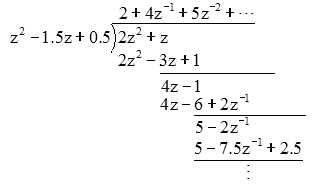
Mathematically, it can be represented as;
$$x(n) = Z^{-1}X(Z)$$where x(n) is the signal in time domain and X(Z) is the signal in frequency domain.
Inverse Z Transform Examples
If we want to represent the above equation in integral format then we can write it as
$$x(n) = (frac{1}{2Pi j})oint X(Z)Z^{-1}dz$$Here, the integral is over a closed path C. This path is within the ROC of the x(z) and it does contain the origin.

Methods to Find Inverse Z-Transform
When the analysis is needed in discrete format, we convert the frequency domain signal back into discrete format through inverse Z-transformation. We follow the following four ways to determine the inverse Z-transformation.
- Long Division Method
- Partial Fraction expansion method
- Residue or Contour integral method
Long Division Method
In this method, the Z-transform of the signal x (z) can be represented as the ratio of polynomial as shown below;
$$x(z)=N(Z)/D(Z)$$Now, if we go on dividing the numerator by denominator, then we will get a series as shown below
$$X(z) = x(0)+x(1)Z^{-1}+x(2)Z^{-2}+...quad...quad...$$The above sequence represents the series of inverse Z-transform of the given signal (for n≥0) and the above system is causal.
However for n<0 the series can be written as;
 $$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...quad...quad...$$
$$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...quad...quad...$$Partial Fraction Expansion Method
Here also the signal is expressed first in N (z)/D (z) form.
If it is a rational fraction it will be represented as follows;
$x(z) = b_0+b_1Z^{-1}+b_2Z^{-2}+...quad...quad...+b_mZ^{-m})/(a_0+a_1Z^{-1}+a_2Z^{-2}+...quad...quad...+a_nZ^{-N})$
The above one is improper when m<n and an≠0
If the ratio is not proper (i.e. Improper), then we have to convert it to the proper form to solve it.
S To Z Transform
Residue or Contour Integral Method
Z Transform Table

In this method, we obtain inverse Z-transform x(n) by summing residues of $[x(z)Z^{n-1}]$ at all poles. Mathematically, this may be expressed as
Z Transform Formula
$$x(n) = displaystylesumlimits_{allquad polesquad X(z)}residuesquad of[x(z)Z^{n-1}]$$Here, the residue for any pole of order m at $z = beta$ is